(Frank Wyrowski教授)
November 2024
摘要
這篇文章探討了近年來備受關注的超透鏡(metalenses)這一主題。超透鏡是平面透鏡的一種特殊類別,與繞射透鏡和菲湼爾透鏡並列。我們介紹了相關概念,並展示了 VirtualLab Fusion軟體在模擬和設計超透鏡方面的能力。所介紹的技術和功能計畫於 2025年發佈。如需獲取更多發佈詳情或關於超透鏡設計與建模的諮詢,請聯繫 support@infotek.com.cn。
本文章源自 2024 年 5 月 29 日在 Photonics Media 網路研討會上,Frank Wyrowski 主持的 “關於超透鏡的討論” (Let’s Talk About Metalenses)講座的文字記錄和演示文稿。
第一章節 介紹
幻燈片 #4–5
LightTrans International開發了 VirtualLab Fusion 光學軟體,並通過全球分銷網路進行推廣。VirtualLab Fusion 是一個多尺度光學模擬平臺,旨在處理各種光學和光子學應用,平面透鏡只是其中的一個示例。本文章重點介紹了 VirtualLab Fusion 在平面透鏡領域的潛力。作為軟體發展商,我們的責任是為不斷擴展的客戶群體提供強大的設計和建模工具,以評估和應用超透鏡(metalenses)及其他平面透鏡于實際應用中。在本文中,我們探討了在軟體發展過程中,將平面透鏡集成到透鏡系統的建模與設計中所面臨的特定任務和挑戰。
幻燈片 #6–7
由於光學軟體依賴於精確且可靠的模擬模型,作為開發者,我們必須深入研究該主題,並全面理解其基本物理原理。這不可避免地涉及一些數學分析和方程式,它們對於嚴謹的討論至關重要。然而,由於這些數學技術已被集成到 VirtualLab Fusion 中,因此使用該軟體進行實際任務的使用者無需掌握相關的基礎物理知識。
除了理論概念的探討之外,本文章還將包含多個模擬和設計示例。在結束這段介紹時,我們希望強調,LightTrans International 在平面透鏡(包括超透鏡(metalenses))的重要性問題上保持中立立場。我們的使命是為您提供強大的軟體工具,使您能夠在工作中探索平面透鏡技術的意義和應用。
圖1:幻燈片#6
第二章節 多尺度的光學模擬
幻燈片 #9–10
超表面(Metasurfaces)利用具有高折射率的奈米結構(通常稱為meta-atoms或者metacells),排列在折射率較低的基底上。這一方法早已被提出 [2],但近年來再次引起廣泛關注 [3]。如果希望對該領域有初步深入的瞭解,建議閱讀 Lalanne 和 Chavel 撰寫的綜述文章 [4]。此外,還推薦 Yang Fan 等人 撰寫的教程 [6],其中包含大量補充參考資料。
幻燈片 #11–12
由於超表面(metasurfaces)由奈米結構組成,顯然幾何光學方法並不適用。相反,必須採用基於麥克斯韋方程組(Maxwell’s equations)的電磁場理論,即通常所稱的物理光學(physical optics)。因此,在透鏡系統中整合超透鏡(metalenses)或其他平面透鏡,與傳統透鏡曲面及其他光學元件結合,會形成一個多尺度系統(multiscale system)。這就需要一種跨尺度的光學建模方法,通常稱為多尺度光學模擬(multiscale optical simulation)。簡單來說,必須強調的是:多尺度模擬無法僅通過資料介面將多個光學軟體工具連接在一起實現。 相反,它需要一個全面的策略,基於高階物理光學理論,為光學軟體提供堅實的理論基礎。對不同尺度的光學系統進行建模,需要在統一的物理光學框架內集成多種不同的模擬模型。這正是我們在 VirtualLab Fusion 軟體中所採用的方法。
圖2:幻燈片#14
幻燈片 #13–15
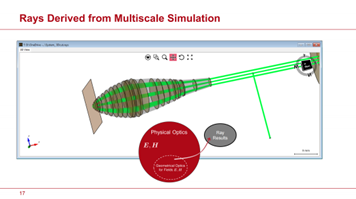
在 VirtualLab Fusion 的眾多技術創新中,幾何光學在電磁場建模方面的進步使其能夠順利與其他物理光學模擬技術相結合。為了實現這一目標,我們遵循了 Max Born 和 Emil Wolf 數十年前提出的指導原則 [1],他們曾強烈建議將幾何光學的基礎擴展至電磁場。通過採用我們統一的多尺度模擬(multiscale simulation)方法,可以無縫銜接傳統透鏡曲面的幾何光學建模與超透鏡(metalens)的高級模擬模型。這種方法在 VirtualLab Fusion 中實現了前所未有的多尺度模擬速度。
圖3:幻燈片#17
幻燈片 #22
在 VirtualLab Fusion 的多尺度模擬框架中,整合超透鏡(metalenses)的主要挑戰在於創建一個能夠與其他光學元件(如傳統透鏡)的模擬模型無縫交互的超透鏡模擬模型。在探討我們如何應對這一挑戰之前,我們需要先回答一個關鍵問題:將平面透鏡集成到光學設計中,預期會帶來哪些結果?
第三章節 超透鏡的潛在應用
幻燈片 #24–29
為了解答這個問題,我們首先做出一些基本觀察。為了生成物點圖像,例如軸向物點圖像,我們設計一個合適的曲面。將這個曲面替換為平面透鏡不會改變物面和像面的距離。因此,平面透鏡的形狀變化不會減少系統的長度。接下來,我們添加另一個物點,這需要一個不同的曲面來實現精確成像。單一曲面無法準確成像多個物點。因此,增加更多的曲面來校正像差是至關重要的,這在透鏡設計中是一個公認的概念。目前沒有證據表明平面透鏡可以消除這一需求。為了進一步理解,我們考慮一個光束擴展器的設計。在這種情況下,初始透鏡用於將入射平面相位轉換為聚焦或發散的球面相位。以發散情況為例。第二個透鏡用於將入射光準直。因此,需要使用兩個透鏡。光束擴束的程度由透鏡間的距離 d 和它們的數值孔徑決定。平面透鏡的使用並不會改變這一結果。
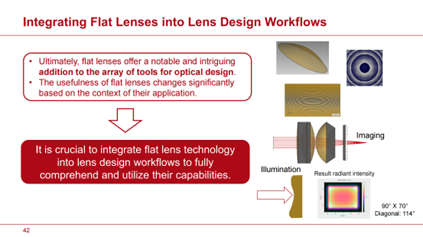
圖4:幻燈片#42
幻燈片 #30–40
基於這些觀察和其他因素,我們得出以下結論:
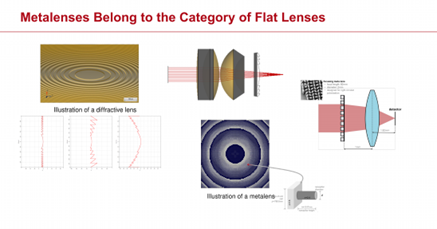
 平面透鏡能夠減少透鏡的厚度和重量。平面透鏡的薄型設計為縮短透鏡表面間距提供了更多可能性。傳統透鏡表面的厚度限制了透鏡表面彼此之間的最小距離,而這一限制在平面透鏡中可以去除。 平面透鏡能夠減少透鏡的厚度和重量。平面透鏡的薄型設計為縮短透鏡表面間距提供了更多可能性。傳統透鏡表面的厚度限制了透鏡表面彼此之間的最小距離,而這一限制在平面透鏡中可以去除。
 平面透鏡的製造方法不同于傳統透鏡,這在某些特定場景下可能帶來好處。 平面透鏡的製造方法不同于傳統透鏡,這在某些特定場景下可能帶來好處。
 平面透鏡可能為可切換透鏡提供新的機會。將厚透鏡表面替換為平面表面,改變了系統中的像差動態,這可能增強基於特定場景的像差校正能力。使用具有強烈對立色差的繞射透鏡來對抗平滑透鏡表面的色差,就是這一潛力的一個典型例子。 平面透鏡可能為可切換透鏡提供新的機會。將厚透鏡表面替換為平面表面,改變了系統中的像差動態,這可能增強基於特定場景的像差校正能力。使用具有強烈對立色差的繞射透鏡來對抗平滑透鏡表面的色差,就是這一潛力的一個典型例子。
 平面透鏡的一些特性,如其偏振敏感功能,可能被視為有益或有害,具體取決於使用場景。本文後續將展示一個例子,說明偏振敏感性的應用。 平面透鏡的一些特性,如其偏振敏感功能,可能被視為有益或有害,具體取決於使用場景。本文後續將展示一個例子,說明偏振敏感性的應用。
 綜合這些觀察,沒有跡象表明平面透鏡(包括超表面透鏡)在縮短光學系統的總長度或減少透鏡表面數量方面,能超越非球面和自由曲面的能力。 綜合這些觀察,沒有跡象表明平面透鏡(包括超表面透鏡)在縮短光學系統的總長度或減少透鏡表面數量方面,能超越非球面和自由曲面的能力。
幻燈片 #41–42
這意味著平面透鏡的纖薄輪廓是其在小型化方面潛力的關鍵因素,沒有更多,也沒有更少。歸根結底,平面透鏡為光學設計工具陣列提供了一個顯著且引人注目的補充。平面透鏡的有效性會根據其應用背景發生顯著變化。總而言之,為了全面理解並充分利用其能力,將平面透鏡技術融入透鏡設計工作流程是至關重要的。現在是時候實際評估平面透鏡的潛力,而不只是單純的進行理論討論。
如前所述,將超透鏡(metalenses)整合到多尺度建模框架中的主要挑戰是創建一個能夠與其他光學元件(如傳統透鏡)的模擬模型無縫交互的超透鏡模擬模型。接下來,我們將探討解決這一挑戰的方法。
第四章 超透鏡的交交互操作模擬模型
透鏡系統將源自物點的波前轉換為創建像點的波前。波前可以通過其對應的相位函數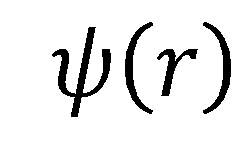 來以數學的方式表示,我們稱之為波前相位。波前相位在透鏡系統的設計和模擬中具有至關重要的作用。 來以數學的方式表示,我們稱之為波前相位。波前相位在透鏡系統的設計和模擬中具有至關重要的作用。
幻燈片 #45
在幾何光學中,波前相位通過以下方程與局部光線方向向量直接相關:
其中,⊥ 表示x和 y 分量,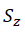 由 由 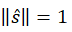 決定。 決定。
幻燈片 #46
(1)
在物理光學中,波前相位保持著至關重要的意義。我們可以將波前相位通過下式集成到電場向量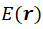 中: 中:
以及
其分量 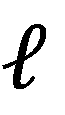 =x,y,z。在多尺度光學模擬中,波前相位 被用作一個連續且平滑的相位,在所有的光學元件中。電場分量可以具有額外的相位,例如與角動量束相關的渦旋相位。 =x,y,z。在多尺度光學模擬中,波前相位 被用作一個連續且平滑的相位,在所有的光學元件中。電場分量可以具有額外的相位,例如與角動量束相關的渦旋相位。
幻燈片 #47
例如,經過傳播後的高斯-拉蓋爾(0,1)光束的相位可以分解為球面波前相位和相位位差。將波前相位與電場分量的其他相位貢獻分離開來,是賦予 VirtualLab Fusion 特殊透鏡建模能力的幾個概念之一。
幻燈片 #48
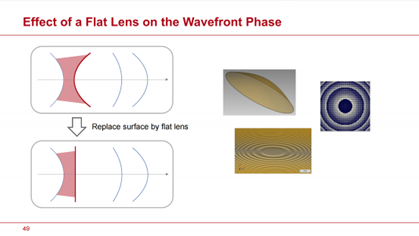
接下來,我們考察透鏡是如何改變波前相位的。常規透鏡通過其表面之間的光程(OPL)來改變波前相位。相位由光程通過以下關係得到:
這個結果在物理光學領域同樣有效。所得相位是連續的,並且沒有以2π形式表示,也就是說,它是展開的。波前相位 的變化與電場的偏振無關!從模擬角度來看,這代表了一個非常寬鬆的數值情形。
圖5:幻燈片#49
幻燈片 #49–52
現在我們考慮涉及平面透鏡的情況。平面透鏡對其平面表面上任意位置的場的影響可以通過以下公式表徵:
為電場的垂直分量。矩陣 是一個二次矩陣,表示為:
在隨後的討論中,電場的z分量不相關,為了簡便起見,我們省略了符號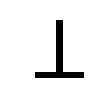 。矩陣 。矩陣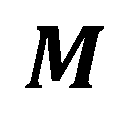 的值可以通過任何合適的平面透鏡表面模擬模型獲得。關於平面透鏡表面結構的具體決策以及適當的模擬模型將在本文稍後討論。現在,我們集中討論平面透鏡對入射場波前相位的影響。關於平面透鏡對波前相位的影響的後續分析適用於任何類型的平面透鏡和為矩陣 的值可以通過任何合適的平面透鏡表面模擬模型獲得。關於平面透鏡表面結構的具體決策以及適當的模擬模型將在本文稍後討論。現在,我們集中討論平面透鏡對入射場波前相位的影響。關於平面透鏡對波前相位的影響的後續分析適用於任何類型的平面透鏡和為矩陣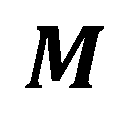 選擇的模擬模型。因此,我們繼續進行這一分析。 選擇的模擬模型。因此,我們繼續進行這一分析。
圖6:幻燈片#54
幻燈片 #53
入射場的波前相位? 可以從矩陣乘法中明確分離出來,得到如下運算式:
其中
相位Ψ表示由平面透鏡引起的入射波前相位的變化。在平面透鏡的情況下,相位 Ψ不是由透鏡表面之間的光程差(OPL)決定的,而必須從矩陣對入射場的影響中推導出,表示為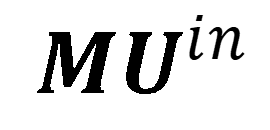 。鑒於相位Ψ在透鏡建模以及設計中的關鍵重要性,必須開發一種穩健的方法,通過 。鑒於相位Ψ在透鏡建模以及設計中的關鍵重要性,必須開發一種穩健的方法,通過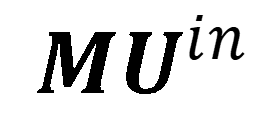 來計算Ψ。 來計算Ψ。
圖7:幻燈片#56
幻燈片 #54–55
定義矩陣 的關鍵因素,進而定義波前相位回應Ψ,包括由參數向量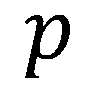 定義的局部結構,在這裡表示為兩種類型的超透鏡單元,局部入射方向 定義的局部結構,在這裡表示為兩種類型的超透鏡單元,局部入射方向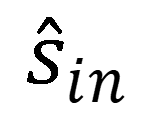 以及波長 以及波長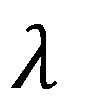 。需要強調的是,在物理光學和幾何光學中,局部方向向量的確定方式是相同的。為了總結我們對矩陣依賴關係的理解,我們將矩陣表示為結構參數、局部入射方向向量和波長的函數。從數學上講,矩陣的依賴關係表示為 。需要強調的是,在物理光學和幾何光學中,局部方向向量的確定方式是相同的。為了總結我們對矩陣依賴關係的理解,我們將矩陣表示為結構參數、局部入射方向向量和波長的函數。從數學上講,矩陣的依賴關係表示為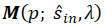 。 。
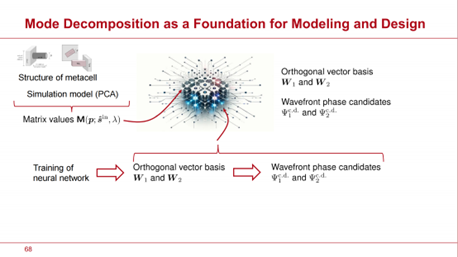
在超透鏡建模和設計領域,深入理解矩陣的值至關重要。這些知識橫跨參數空間、方向域和波長範圍。我們希望強調的是,任何在光學軟體領域中沒有使用完整建模矩陣來涵蓋必要的結構參數、方向和波長範圍的方法,都不具備足夠先進的能力來提供研究平面光學潛力所需的工具。因此,我們在參數空間內計算選定類型的超透鏡單元結構、相關方向域和應用波長範圍的所有矩陣值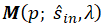 。這些矩陣值作為神經網路中的節點,連接參數空間、方向域和波長範圍。該神經網路封裝了用於具有特定超透鏡單元配置的超透鏡的所有建模和設計資料。 。這些矩陣值作為神經網路中的節點,連接參數空間、方向域和波長範圍。該神經網路封裝了用於具有特定超透鏡單元配置的超透鏡的所有建模和設計資料。
幻燈片 #56
需要注意的是,這個神經網路對於每種類型的超透鏡單元結構只需要計算一次。在典型的筆記型電腦上使用先進的建模方法,根據涉及的節點數量,設置神經網路所需的時間從幾小時到幾天不等,。VirtualLab Fusion 支持分散式運算,這使得隨著更多用戶端的加入,計算時間幾乎呈線性減少。總之,網路計算在平面光學建模和設計中並不是一個實際限制。接下來,我們將假設神經網路已經建立並準備好提供所有關於矩陣元素的必要細節。
圖8:幻燈片#49 metacells結構的計算
幻燈片 #57
在神經網路建立後,我們現在著手確定超透鏡的波前相位響應的任務。首先,我們必須理解面前這個任務的本質。為了清晰起見,討論將集中在單一波長上。給定特定的Uin,神經網路提供了振幅:
以及相位:
幻燈片 #58-62
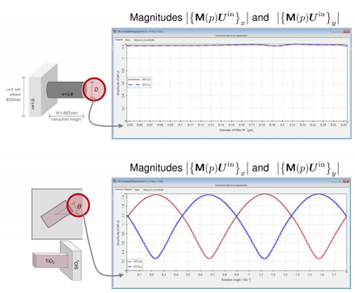
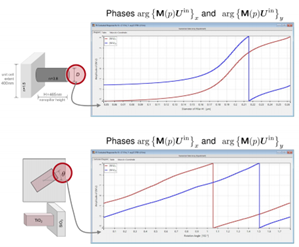
接下來,我們考察多種情景,其中使用基於圖 8 中規格的兩種類型的超透鏡單元,並結合不同的輸入偏振。在這個初步示例中,如圖 9 所示,我們使用線偏振光來評估柱狀超透鏡單元和奈米柱超透鏡單元的振幅結果,每個單元都由不同的結構參數特徵化。圖 11 描述了相位。奈米柱結構的結果顯示,x 和 y 分量之間存在顯著差異,而柱狀單元則沒有這種差異。接下來,我們將入射光從線偏振改為圓偏振,並考察由此產生的振幅和相位結果。結果如圖 11 和 12 所示。兩種超透鏡單元類型的 x 和 y 分量的相位值曲線似乎主要是偏移的,但在其他方面保持相似或幾乎相同。圖 9-12 中呈現的資料表明,考慮到超透鏡單元中的偏振效應通常是至關重要的。這引出了一個問題,即應當決定哪個相位應該被識別並處理為波前相位回應Ψ。x 和 y 分量是兩個明顯的選擇。然而,如果它們有所不同,該如何處理呢?
圖9:此圖展示了場與左側的metacells相互作用後,其 x 分量和 y 分量大小的變化情況。這種變化是通過在整個指定範圍內改變結構參數來實現的。場的輸入向量為 Uin = (1, 1)T,表示線偏振光。初始方向為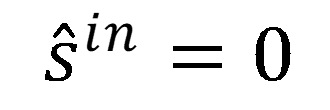 。超單元的結構規格用於示例計算。詳見第 59 張幻燈片。 。超單元的結構規格用於示例計算。詳見第 59 張幻燈片。
從數學角度來看,我們必須選擇一個合適的候選波前相位響應 Ψc.c.,並從矩陣乘法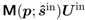 的結果中提取它。因此,我們得到殘餘相位分量: 的結果中提取它。因此,我們得到殘餘相位分量:
其中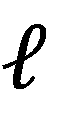 =x,y。候選波前相位的品質應基於殘餘相位的大小來評估,同時考慮各個分量的幅值。無需深入定義,我們僅需說明,我們採用一個關於相位殘差的次級動量準則來評估候選方案的品質。品質評價標準由單個σ2值表示。 =x,y。候選波前相位的品質應基於殘餘相位的大小來評估,同時考慮各個分量的幅值。無需深入定義,我們僅需說明,我們採用一個關於相位殘差的次級動量準則來評估候選方案的品質。品質評價標準由單個σ2值表示。
圖 13 展示了之前示例的評價值。該表給出了前面討論的示例σ2的值,使用矩陣乘法結果中 x 分量或 y 分量的相位作為波前相位候選。
圖10:此圖展示了場與左側的metacells相互作用後,其 x 分量或 y 分量的相位大小的變化情況。這種變化是通過在整個指定範圍內改變結構參數來實現的。場的輸入向量為 Uin = (1,i)T,表示線偏振光。初始方向為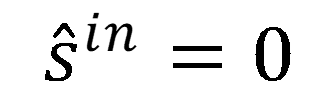 。超單元的結構規格用於示例計算。詳見第 60 張幻燈片。 。超單元的結構規格用於示例計算。詳見第 60 張幻燈片。
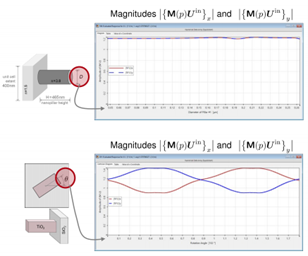
圖11:此圖展示了場與左側的metacells相互作用後,其 x 分量和 y 分量大小的變化情況。這種變化是通過在整個指定範圍內改變結構參數來實現的。場的輸入向量為 Uin = (1,i)T,表示圓偏振光。初始方向為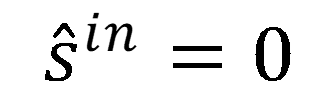 。超單元的結構規格用於示例計算。詳見第 61 張幻燈片。 。超單元的結構規格用於示例計算。詳見第 61 張幻燈片。
圖12:此圖展示了場與左側的metacells相互作用後,其 x 分量和 y 分量大小的變化情況。這種變化是通過在整個指定範圍內改變結構參數來實現的。場的輸入向量為 Uin = (1,1)T,表示圓偏振光。初始方向為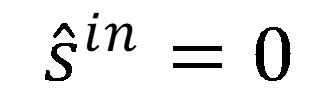 。超單元的結構規格用於示例計算。詳見第 62 張幻燈片。 。超單元的結構規格用於示例計算。詳見第 62 張幻燈片。
σ2值清楚地表明瞭奈米柱結構對偏振的顯著依賴性。顯然,線上偏振情況下,這兩種候選方案對於奈米柱超元胞而言都是不合適的,若沒有合適的波前相位,金屬透鏡的設計將不可行!這一結果明確說明,簡單地選擇矩陣乘法結果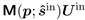 中的 x 或 y 分量作為波前相位的方法,並不足以支撐金屬透鏡的設計與建模,特別是在嚴肅的軟體發展過程中。這種過於簡化的方法無法提供穩健且可靠的基礎,進一步凸顯了更複雜和精細的方法對於實現可行且有效的金屬透鏡建模與設計的必要性。因此,我們提出了一種超透鏡設計與模擬技術,該方法充分利用了成熟的神經網路能力,以優化設計流程並提高模擬的精確度。 中的 x 或 y 分量作為波前相位的方法,並不足以支撐金屬透鏡的設計與建模,特別是在嚴肅的軟體發展過程中。這種過於簡化的方法無法提供穩健且可靠的基礎,進一步凸顯了更複雜和精細的方法對於實現可行且有效的金屬透鏡建模與設計的必要性。因此,我們提出了一種超透鏡設計與模擬技術,該方法充分利用了成熟的神經網路能力,以優化設計流程並提高模擬的精確度。
幻燈片 #66-67
需要注意的是,網路中的節點由矩陣值表示,這些矩陣值是基於選定的超元胞幾何結構和參數空間計算得出的。為了進行此類計算,必須使用合適的模擬模型。
鑒於每個超元胞(meta-atom)都被相鄰的超元胞所包圍,因此矩陣分析並非針對單個孤立的超元胞進行,而是基於週期性重複的超元胞進行分析。這種週期性重複形成了一個亞波長光柵,其中超元胞作為週期單元用於分析。
對該超元胞光柵的分析採用傅立葉模態法(Fourier Modal Method, FMM),也稱為嚴格耦合波分析法(Rigorous Coupled-Wave Analysis, RCWA)。
圖13:表中的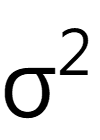 值用於評估相位回應品質。較低的值與較高的值相比性能更好。詳見第66張幻燈片。 值用於評估相位回應品質。較低的值與較高的值相比性能更好。詳見第66張幻燈片。
圖14:該表顯示了兩種metacell配置的向量基,來源於訓練神經網路。詳見第69張幻燈片。
我們將這種有效的技術稱為週期單元近似(Periodic Cell Approximation,PCA)。在第 7 和第 8 節中,我們將探討 PCA 的精度,並展示如何改進超結構的模擬,以建立神經網路。在本節接下來的討論中,我們採用 PCA 方法。然而,即使選擇其他方法,所有討論和結論仍然適用。
幻燈片 #68–69
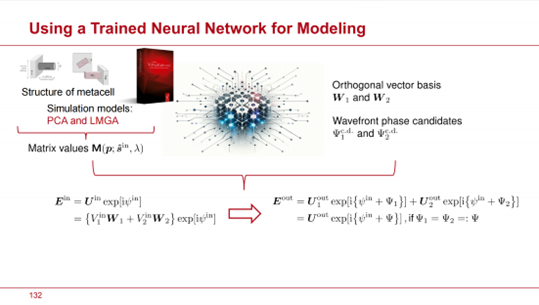
在下一步中,我們訓練神經網路,以識別正交向量基W1和W2,從而通過最小σ2獲得最優的波前相位候選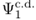 和 和 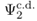 。 。
當神經網路訓練完成後,模式和相位候選結果將嵌入網路中,使其可以直接應用。對我們所研究的兩個示例結構進行訓練後,得到的正交基如表14 所示。作為軟體發展人員,確保這一神經網路訓練概念能提供全自動化技術至關重要。它允許任何用戶選擇一個或多個超元胞幾何結構,並啟動訓練過程,從而生成金屬透鏡建模和設計所需的全部內容。
圖15:幻燈片#68
為了使入射光透過超透鏡,首先需要將初始場分解為神經網路提供的模式,從而得到以下場的運算式
神經網路的訓練已經解決了兩種模式的建模,使我們能夠推導出輸出場:
通常,這個場由兩種模式組成;然而,當偏振依賴性較小,波前相位可能會對齊,從而使單一模式足以代表輸出場。在超透鏡建模中出現兩種模式並不令人驚訝。這種現象也可以在雙折射介質中觀察到。即使在各向同性介質中製造的奈米結構表面,也會觀察到偏振效應,這種效應被稱為形態雙折射[1]。
幻燈片 #71–72
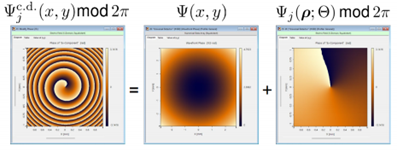
在方程 (13) 中,故意省略了候選符號,因為方程 (13) 中表示的波前回應與神經網路提供的回應之間仍然存在明顯的區別。相位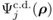 尚未是波前相位的形式,因為它們是以 2π形式呈現的。此外,它們可能包含一些不屬於平滑波前相位的成分,例如,如圖 16 所示,它們無法像渦旋相位那樣展開。因此,在最終步驟中,相位 尚未是波前相位的形式,因為它們是以 2π形式呈現的。此外,它們可能包含一些不屬於平滑波前相位的成分,例如,如圖 16 所示,它們無法像渦旋相位那樣展開。因此,在最終步驟中,相位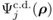 被展開並濾波。我們將此操作稱為Θ,並得到 被展開並濾波。我們將此操作稱為Θ,並得到
圖16:候選相位和所得波前相位回應之間的差異示例。另見幻燈片 #71
該方法依賴於 Badar [5] 探索的樣條插值技術。通過這一展開和濾波過程,兩個模式 j 的輸出場可以表示為:
通過平滑和解包裹後的相位為:
第五張章 超透鏡設計
幻燈片 #74
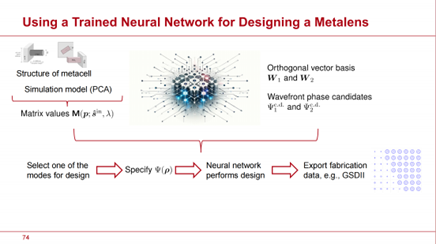
接下來,我們將探討以訓練後的神經網路為基礎創建超透鏡的方法。該設計僅適用於一種模式,前提是這些模式具有不同的波前相位回應。因此,必須選擇其中一種模式進行設計。對於該模式,超透鏡預計將產生指定的波前響應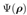 。因此,首先必須選擇這一波前回應。可以通過多種在透鏡設計中常見的方法實現這一點,例如配置薄透鏡系統。另一種方法是從透鏡系統中選擇一個厚透鏡表面,然後用超透鏡替代。在這種情況下,VirtualLab Fusion 可以確定所需的波前相位回應 。因此,首先必須選擇這一波前回應。可以通過多種在透鏡設計中常見的方法實現這一點,例如配置薄透鏡系統。另一種方法是從透鏡系統中選擇一個厚透鏡表面,然後用超透鏡替代。在這種情況下,VirtualLab Fusion 可以確定所需的波前相位回應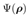 。 。
設計過程可以完全交由神經網路來完成,因為它包含了產生相位值與超元胞內結構參數之間關係的全面資訊。在設計階段,每個超元胞的結構參數會根據其在平面透鏡表面上的位置來確定。在最後階段,製造資料(例如 GSDII 格式)將被生成。
圖17:幻燈片#74
幻燈片 #75
模擬和設計技術已經整合到我們專有的 VirtualLab Fusion 軟體中。這些先進的技術計畫將在即將發佈的 2025 年軟體更新中向公眾推出。接下來,我們將深入探討一些通過我們專有的 VirtualLab Fusion 軟體完成的真正出色的示例演示。
第六章 設計示例和模擬
幻燈片 #77
我們從柱形聚焦超透鏡開始。在這裡,您可以找到透鏡的規格以及 GDSII 資料的一個片段。通過使用神經網路,透鏡設計在兩秒鐘內完成。約有 7500 x 7500 個超元胞排列在直徑為三毫米的透鏡上。
幻燈片 #78
系統中的光線分佈是多尺度模擬的一個結果。
幻燈片 #79–82
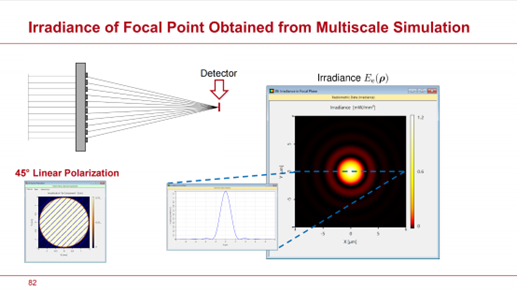
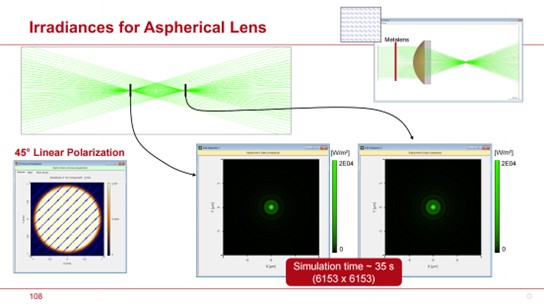
模擬還提供了在焦平面上依賴於輸入場偏振的場強和輻照度的大小。在這個示例中,和所有後續示例一樣,模擬時間大約在 10 秒至不到一分鐘之間,運行在標準筆記型電腦上。PCA 模型效率大約為 94%。我們將在第 7 節中觀察到,這個估計值有些過於樂觀。
圖18:幻燈片#82
幻燈片 #83–84
通過使用神經網路仔細分析超透鏡的波前相位響應,我們還可以檢查在使用離軸輸入場時,超透鏡引起的像差。
圖19:幻燈片#87
幻燈片 #85–88
對於離軸平面輸入場,多尺度模擬提供了點圖、場強和焦平面上的輻照度。
幻燈片 #89–94
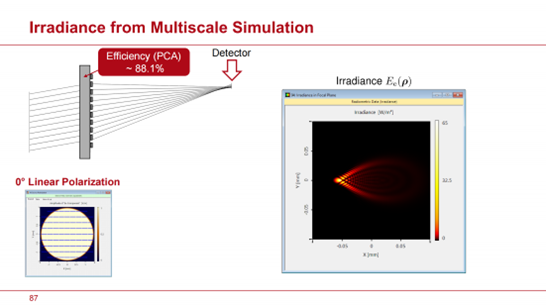
接下來,我們將柱型超元胞替換為奈米鰭型超元胞。設計針對其中一個正交模式,這裡是針對右旋圓偏振場。然後,進行與柱型超元胞相似的模擬。我們獲得了透鏡後的光線分佈和場強。由於高頻調製,莫爾條紋效應導致圖像呈現出一些不尋常的外觀。仔細檢查後發現了高頻調製。這是由於參數空間中的振幅調製所引起的,我們在討論神經網路時已經提到過。該調製導致效率略有下降。焦平面上的場強和輻照度也可以很容易地計算出來。
圖20:幻燈片#99
幻燈片 #95–96
現在,我們將圓偏振輸入從右旋改為左旋,光線分佈的變化清晰可見。透鏡表現出發散行為!在與之前相同的平面上計算輻照度確認了這一結果。
幻燈片 #97–101
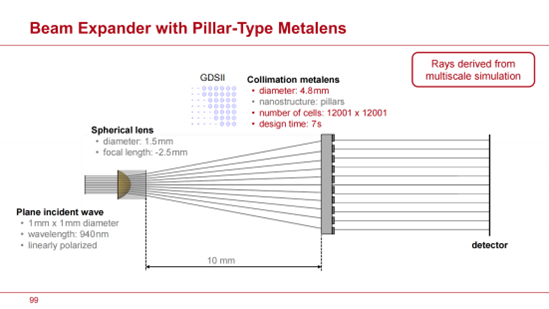
在下一個示例中,我們在光束擴束器系統中用柱型超透鏡替換了一個非球面透鏡表面。在選擇要替換的表面後,VirtualLab Fusion 自動確定超透鏡所需的相位回應。超透鏡的直徑接近 5 毫米,由 12000 x 12000 個超元胞組成,確保其功能性。訓練後的神經網路在 7 秒鐘內完成設計。通過透鏡後的輻照度和計算的向量點擴展函數(PSF)展示了超透鏡的性能。
幻燈片 #101–104
在結束模擬示例時,我們展示了一個設計,其中利用奈米鰭超元胞結構的兩種模式創建了一個雙焦透鏡系統。我們首先從金屬透鏡後方放置一個球面透鏡。接著,多尺度模擬方法提供了光線結果,顯示了兩種模式的明顯球面像差。這個示例展示了我們的方法使得將超透鏡整合到光學透鏡系統中成為可能,並提供了對像差分析的全面訪問。
圖21:幻燈片#108
幻燈片 #105–109
接下來,我們設計了一個合適的非球面透鏡並再次進行實驗。對於右旋圓偏振模式,焦點出現在第一個探測器位置。當切換到左旋圓偏振模式時,焦點移動到第二個位置。當輸入光為線性偏振時,輸出中會產生兩種模式,從而形成兩個焦點。超透鏡允許額外編碼相位位移,導致焦點中心的輻照度降至零。
提供的這些示例展示了我們先進的超透鏡技術的能力,該技術已被開發並整合到 VirtualLab Fusion 中,計畫於 2025 年公開發佈。
第七章 PCA 模擬模型的局限性及其進一步發展
幻燈片 #111–114
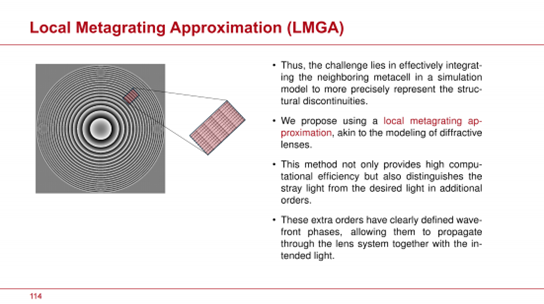
接下來,我們對週期單元近似(PCA)進行更為深入和批判性的審視。在 PCA 中,假設鄰近的超元胞是相同的。實際上,每個超元胞都被額外的超元胞包圍,這些超元胞在結構參數上存在不同程度的差異,從而在一定程度上破壞了週期單元的條件。這種情況特別出現在透鏡區段的一個週期完成時,導致結構參數回到其初始值。這會導致結構中的不連續性,進而產生額外的散射光,這一現象在繞射透鏡中也得到了廣泛的認識。因此,挑戰在於有效地將鄰近超元胞整合到模擬模型中,以更精確地表示結構的不連續性。對於這樣的模型,關鍵是要考慮結構的躍變。僅僅包括直接相鄰結構並不足以提高精度。我們建議使用局部超光柵近似(LMGA),類似於繞射透鏡的建模方法。這種方法不僅提供了高計算效率,而且能夠在額外的繞射階次中區分散射光與期望光。這些額外的繞射階次具有明確定義的波前相位,使得除了預期的光之外,這些光也能夠通過透鏡系統傳播。如果超透鏡被集成到透鏡系統中,這一點尤為重要。此時,必須評估由額外階次繞射光引起的散射光對像平面的影響,例如對點擴展函數(PSF)的影響。
圖22:幻燈片#114
幻燈片 #115
對於分析局部光柵,我們採用嚴格的傅立葉模方法(FMM),也稱為 RCWA。通過生成使用 PCA 構建的超光柵,並隨後使用嚴格的傅立葉模方法和 PCA 進行模擬比較,可以系統地分析 PCA 和 LMGA 之間的結果差異。
幻燈片 #116–129
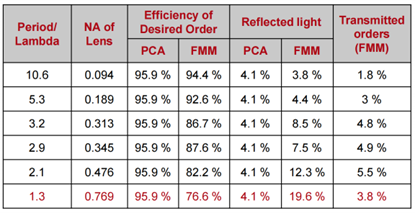
我們已執行這一程式,並在表格 23 中展示了柱型超元胞的結果。我們創建了週期逐漸減小的超光柵,在表中以波長的倍數表示。我們還指定了可以使用此週期設計的透鏡的最大數值孔徑。接下來,我們展示了每個光柵將光引導至預定階次的效率,並對比了使用 PCA 和 FMM 獲得的結果。隨後,我們展示了反射光的相同分析。在最後一列,我們展示了使用 FMM 計算的所有更高傳輸階次的效率。我們展示了計算的波前相位響應的對比,展示了 PCA 和 FMM 的結果,如幻燈片中所述。請考慮從最大週期開始的結果。通過 PCA 獲得的結果與 FMM 的結果非常接近,儘管 FMM 的效率略低。如預期,結構不連續處出現輕微的相位偏差。進一步減小光柵週期驗證了,儘管 PCA 可以很好地預測相位值,但它未能有效地考慮更高反射和傳輸階次中的雜散光。當光柵週期接近光的波長,進入共振區域時,PCA 變得無效。此時,光柵的回應也高度依賴於偏振狀態。局部光柵的共振區域不適合透鏡設計,從而限制了透鏡的最大數值孔徑。
圖23:該表給出了一個比較超光柵繞射效率的概述,使用PCA和LMGA進行分析。光柵都是用PCA設計的。詳見幻燈片第117-129張。
圖24:幻燈片#132
幻燈片 #130-132
我們總結了結果:
• PCA 在局部光柵的共振區域之外,提供了相位建模和設計的高精度。
• PCA 無法預測更高階反射和透射中的雜散光的出現。
• 局部超光柵近似(LMGA)可以實現這一點。
我們計畫在 VirtualLab Fusion 軟體中集成一個工具,用於進行類似於前面示例的光柵分析,適用於任何類型的超光柵,而不受超元胞類型的限制。這樣可以初步瞭解所選超元胞的能力。此外,我們通過將局部超光柵近似(LMGA)模擬模型納入神經網路,增強了神經網路的功能,使其能夠執行擴展的建模。局部光柵近似概念已經被集成並用於 VirtualLab Fusion 中的繞射透鏡設計。
圖25:幻燈片#137
第八章 超透鏡的“魯棒性”
幻燈片 #135–137
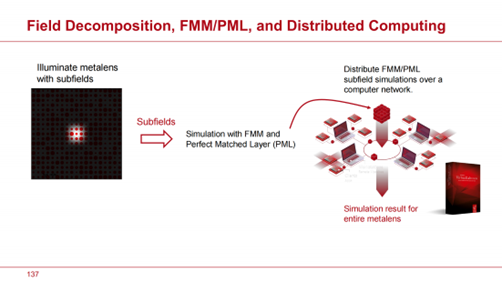
在本文的結尾,我們想簡要概述一下我們進一步推進模型的策略。將PCA和LMGA模擬模型整合到我們的神經網路方法中,提供了在透鏡系統中模擬平面透鏡時,在精度和速度之間的良好平衡。然而,它們並未完全考慮超元胞的具體網格排列。從建模的角度來看,這種現象導致了雜散光的輕微增加,可以解釋為超透鏡內在的“魯棒性”所致。我們希望指出,這種內在的魯棒性在超透鏡建模中與透鏡表面魯棒性和其他缺陷的建模作用類似。我們正在為這兩個方面尋找解決方案,因為這些建模挑戰密切相關。我們方法的核心是分析超透鏡和粗糙表面的散射效應。為此,我們設計了一種結合了完美匹配層(PML)的傅立葉模態法(FMM),該方法利用了入射場的橫向分解以及分散式運算。在我們去年最新發佈的2024版本中,VirtualLab Fusion以非常友好的方式引入了分散式運算。通過將電腦網路中所有用戶端的結果結合起來,可以得到整個超透鏡的模擬結果。這使得能夠對透鏡區域的散射影響進行徹底調查,且區域的大小可以根據分散式運算網路中用戶端的數量進行調整。
我們要強調的是,儘管分析魯棒性及其對透鏡系統性能的影響至關重要,但沒有任何透鏡設計師會因為不確定如何將魯棒性分析納入設計中,而停止使用現有的軟體工具進行透鏡系統設計。這種務實的方法也應當適用於平面透鏡,包括超透鏡。通過VirtualLab Fusion,我們提供了一系列日益擴展的工具和技術,用於精確高效地設計和模擬平面透鏡,幫助您在工作中探索它們的潛力。
第九章 結論
幻燈片 #139
我們想通過重申平面透鏡是光學設計工具包中令人矚目和令人興奮的新成員來結束本文,尤其在成像和照明領域。將平面透鏡技術納入透鏡設計流程,對於全面理解和利用它們的全部潛力至關重要。在本文中,我們概述了我們解決這一挑戰問題的方法。我們解決這一任務的方法得到了VirtualLab Fusion提供的卓越多尺度模擬技術的促進。在即將於2025年發佈的軟體更新中,我們將整合本文展示的平面透鏡技術,允許您直接使用它們。
參考文獻
[1] M. Born and E. Wolf. Principles of optics. 6. Pergamon Press, New York, 1980.
[2] P. Lalanne et al. “Design and fabrication of blazed binary diffractive elements with sampling periods smaller than the structural cutoff”. In: J.\ Opt.\ Soc.\Am.\ A 16.5 (1999), pp. 1143–1156.
[3] Mohammadreza Khorasaninejad et al. “Metalenses at visible wavelengths: Diffractionlimited focusing and subwavelength resolution imaging”. In: Science 352.6290(June 3, 2016), pp. 1190–1194. issn: 0036-8075, 1095-9203. doi: 10 . 1126 /science.aaf6644. url:https://www.science.org/doi/10.1126/science.aaf6644 (visited on 11/15/2024).
[4] Philippe Lalanne and Pierre Chavel. “Metalenses at visible wavelengths: past, present, perspectives”. In: Laser & Photonics Reviews 11.3 (May 2017), p. 1600295.issn: 1863-8880, 1863-8899. doi: 10 . 1002 / lpor . 201600295. url: https :/ / onlinelibrary . wiley . com / doi / 10 . 1002 / lpor . 201600295 (visited on
11/15/2024).
[5] Irfan Badar, Christian Hellmann, and Frank Wyrowski. “Wavefront phase representation by Zernike and spline models: a comparison”. In: Journal of the Optical Society of America A 38.8 (Aug. 1, 2021), p. 1178. issn: 1084-7529, 1520-8532.doi: 10.1364/JOSAA.427519. url: https://opg.optica.org/abstract.cfm?
URI=josaa-38-8-1178 (visited on 09/22/2022).
[6] Fan Yang et al. “Wide field-of-view metalens: a tutorial”. In: Advanced Photonics 5 (May 1, 2023). ADS Bibcode: 2023AdPho...5c3001Y, p. 033001. doi: 10.1117/1.AP.5.3.033001. url:https://ui.adsabs.harvard.edu/abs/2023AdPho...5c3001Y/abstract(visited on 11/15/2024).
|




 平面透鏡能夠減少透鏡的厚度和重量。平面透鏡的薄型設計為縮短透鏡表面間距提供了更多可能性。傳統透鏡表面的厚度限制了透鏡表面彼此之間的最小距離,而這一限制在平面透鏡中可以去除。
平面透鏡能夠減少透鏡的厚度和重量。平面透鏡的薄型設計為縮短透鏡表面間距提供了更多可能性。傳統透鏡表面的厚度限制了透鏡表面彼此之間的最小距離,而這一限制在平面透鏡中可以去除。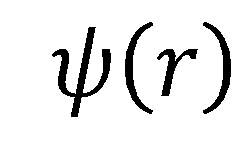 來以數學的方式表示,我們稱之為波前相位。波前相位在透鏡系統的設計和模擬中具有至關重要的作用。
來以數學的方式表示,我們稱之為波前相位。波前相位在透鏡系統的設計和模擬中具有至關重要的作用。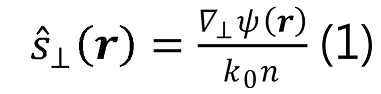
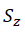 由
由 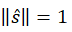 決定。
決定。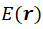 中:
中: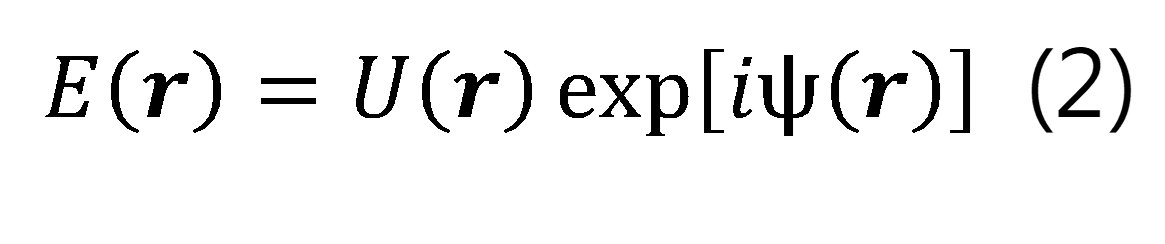
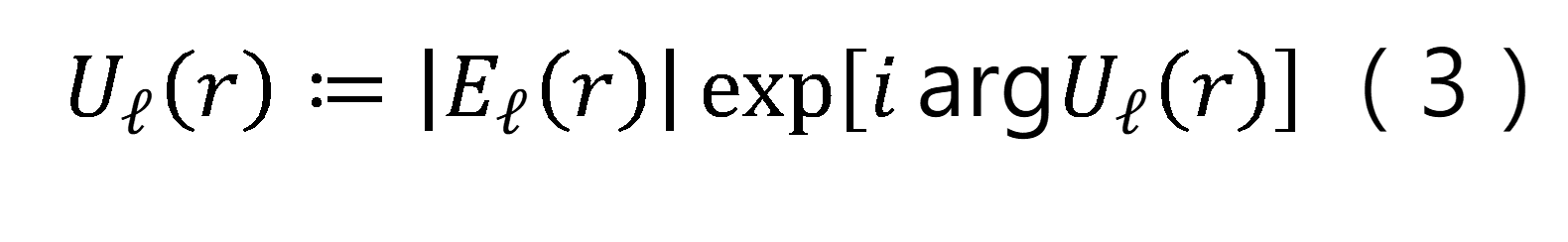
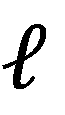 =x,y,z。在多尺度光學模擬中,波前相位 被用作一個連續且平滑的相位,在所有的光學元件中。電場分量可以具有額外的相位,例如與角動量束相關的渦旋相位。
=x,y,z。在多尺度光學模擬中,波前相位 被用作一個連續且平滑的相位,在所有的光學元件中。電場分量可以具有額外的相位,例如與角動量束相關的渦旋相位。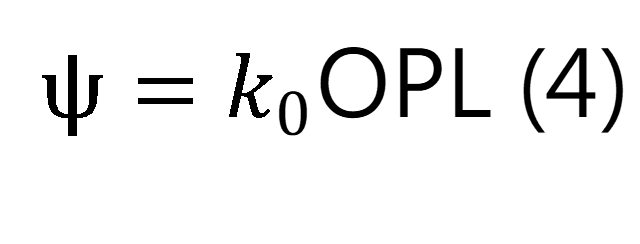
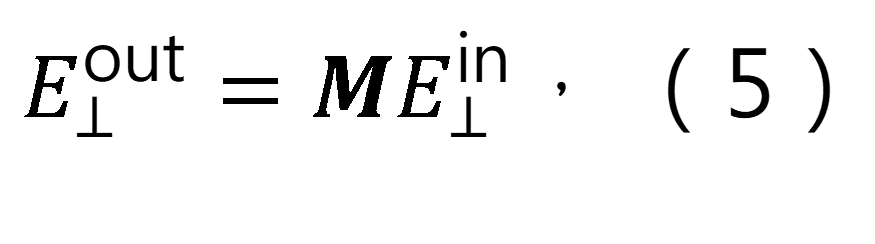
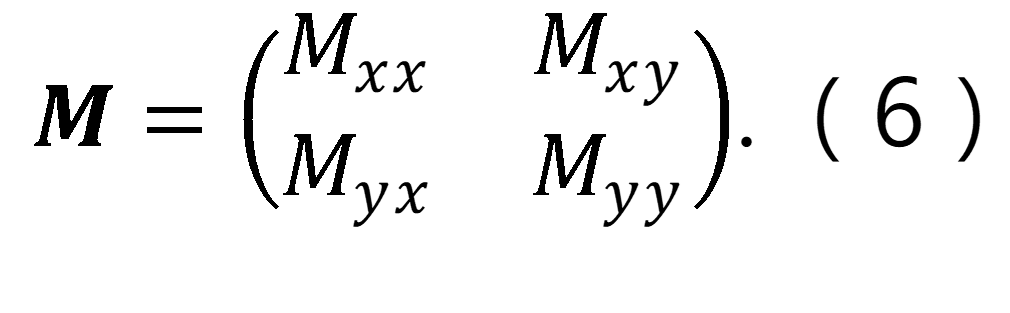
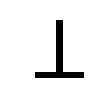 。矩陣
。矩陣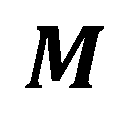 的值可以通過任何合適的平面透鏡表面模擬模型獲得。關於平面透鏡表面結構的具體決策以及適當的模擬模型將在本文稍後討論。現在,我們集中討論平面透鏡對入射場波前相位的影響。關於平面透鏡對波前相位的影響的後續分析適用於任何類型的平面透鏡和為矩陣
的值可以通過任何合適的平面透鏡表面模擬模型獲得。關於平面透鏡表面結構的具體決策以及適當的模擬模型將在本文稍後討論。現在,我們集中討論平面透鏡對入射場波前相位的影響。關於平面透鏡對波前相位的影響的後續分析適用於任何類型的平面透鏡和為矩陣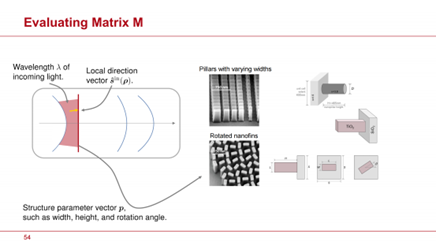
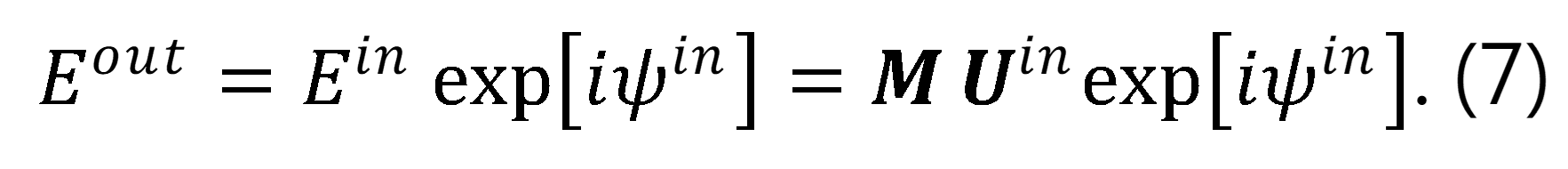
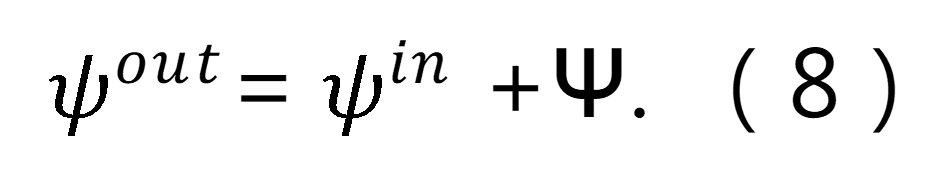
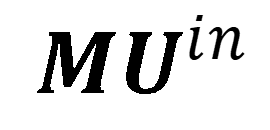 。鑒於相位Ψ在透鏡建模以及設計中的關鍵重要性,必須開發一種穩健的方法,通過
。鑒於相位Ψ在透鏡建模以及設計中的關鍵重要性,必須開發一種穩健的方法,通過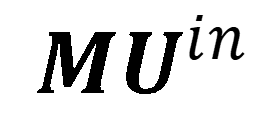 來計算Ψ。
來計算Ψ。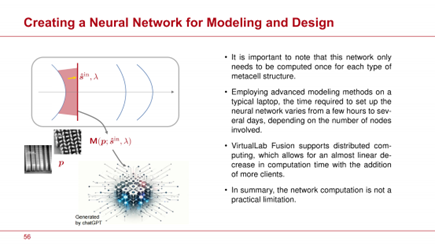
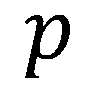 定義的局部結構,在這裡表示為兩種類型的超透鏡單元,局部入射方向
定義的局部結構,在這裡表示為兩種類型的超透鏡單元,局部入射方向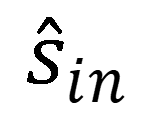 以及波長
以及波長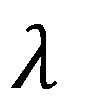 。需要強調的是,在物理光學和幾何光學中,局部方向向量的確定方式是相同的。為了總結我們對矩陣依賴關係的理解,我們將矩陣表示為結構參數、局部入射方向向量和波長的函數。從數學上講,矩陣的依賴關係表示為
。需要強調的是,在物理光學和幾何光學中,局部方向向量的確定方式是相同的。為了總結我們對矩陣依賴關係的理解,我們將矩陣表示為結構參數、局部入射方向向量和波長的函數。從數學上講,矩陣的依賴關係表示為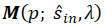 。
。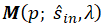 。這些矩陣值作為神經網路中的節點,連接參數空間、方向域和波長範圍。該神經網路封裝了用於具有特定超透鏡單元配置的超透鏡的所有建模和設計資料。
。這些矩陣值作為神經網路中的節點,連接參數空間、方向域和波長範圍。該神經網路封裝了用於具有特定超透鏡單元配置的超透鏡的所有建模和設計資料。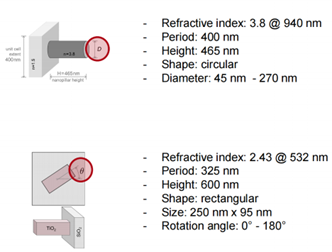
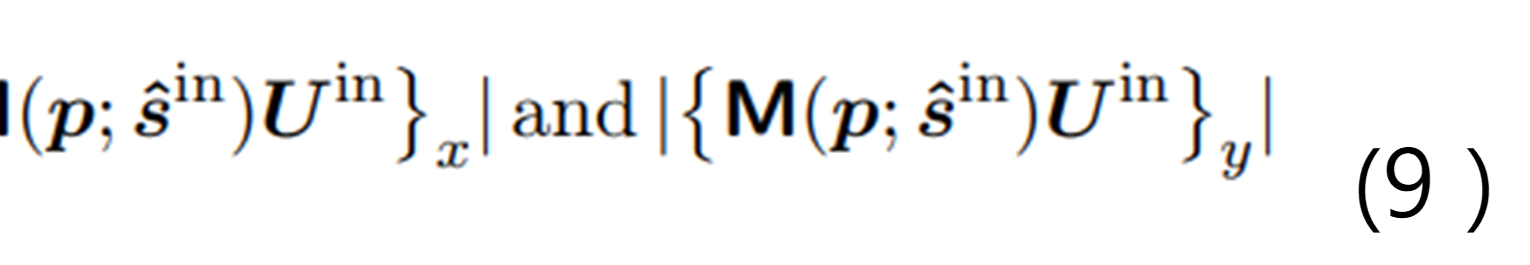

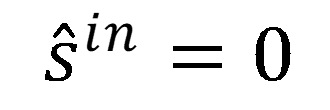 。超單元的結構規格用於示例計算。詳見第 59 張幻燈片。
。超單元的結構規格用於示例計算。詳見第 59 張幻燈片。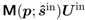 的結果中提取它。因此,我們得到殘餘相位分量:
的結果中提取它。因此,我們得到殘餘相位分量: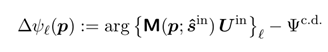
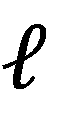 =x,y。候選波前相位的品質應基於殘餘相位的大小來評估,同時考慮各個分量的幅值。無需深入定義,我們僅需說明,我們採用一個關於相位殘差的次級動量準則來評估候選方案的品質。品質評價標準由單個σ2值表示。
=x,y。候選波前相位的品質應基於殘餘相位的大小來評估,同時考慮各個分量的幅值。無需深入定義,我們僅需說明,我們採用一個關於相位殘差的次級動量準則來評估候選方案的品質。品質評價標準由單個σ2值表示。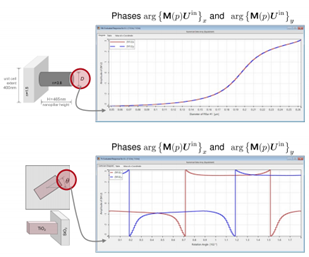
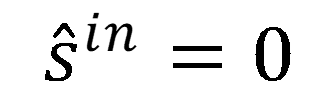 。超單元的結構規格用於示例計算。詳見第 60 張幻燈片。
。超單元的結構規格用於示例計算。詳見第 60 張幻燈片。
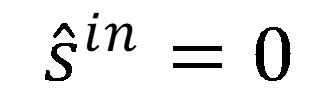 。超單元的結構規格用於示例計算。詳見第 62 張幻燈片。
。超單元的結構規格用於示例計算。詳見第 62 張幻燈片。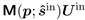 中的 x 或 y 分量作為波前相位的方法,並不足以支撐金屬透鏡的設計與建模,特別是在嚴肅的軟體發展過程中。這種過於簡化的方法無法提供穩健且可靠的基礎,進一步凸顯了更複雜和精細的方法對於實現可行且有效的金屬透鏡建模與設計的必要性。因此,我們提出了一種超透鏡設計與模擬技術,該方法充分利用了成熟的神經網路能力,以優化設計流程並提高模擬的精確度。
中的 x 或 y 分量作為波前相位的方法,並不足以支撐金屬透鏡的設計與建模,特別是在嚴肅的軟體發展過程中。這種過於簡化的方法無法提供穩健且可靠的基礎,進一步凸顯了更複雜和精細的方法對於實現可行且有效的金屬透鏡建模與設計的必要性。因此,我們提出了一種超透鏡設計與模擬技術,該方法充分利用了成熟的神經網路能力,以優化設計流程並提高模擬的精確度。
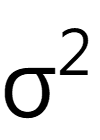 值用於評估相位回應品質。較低的值與較高的值相比性能更好。詳見第66張幻燈片。
值用於評估相位回應品質。較低的值與較高的值相比性能更好。詳見第66張幻燈片。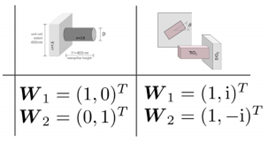
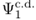 和
和 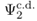 。
。
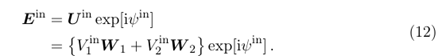
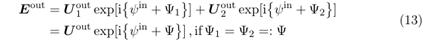
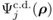 尚未是波前相位的形式,因為它們是以 2π形式呈現的。此外,它們可能包含一些不屬於平滑波前相位的成分,例如,如圖 16 所示,它們無法像渦旋相位那樣展開。因此,在最終步驟中,相位
尚未是波前相位的形式,因為它們是以 2π形式呈現的。此外,它們可能包含一些不屬於平滑波前相位的成分,例如,如圖 16 所示,它們無法像渦旋相位那樣展開。因此,在最終步驟中,相位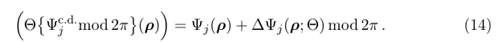
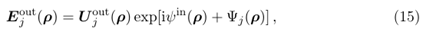
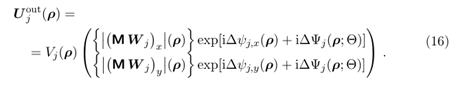
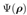 。因此,首先必須選擇這一波前回應。可以通過多種在透鏡設計中常見的方法實現這一點,例如配置薄透鏡系統。另一種方法是從透鏡系統中選擇一個厚透鏡表面,然後用超透鏡替代。在這種情況下,VirtualLab Fusion 可以確定所需的波前相位回應
。因此,首先必須選擇這一波前回應。可以通過多種在透鏡設計中常見的方法實現這一點,例如配置薄透鏡系統。另一種方法是從透鏡系統中選擇一個厚透鏡表面,然後用超透鏡替代。在這種情況下,VirtualLab Fusion 可以確定所需的波前相位回應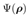 。
。